递归神经网络 RNN 笔记

Posted on   |   In   |     |  

介绍 RNN 及其变种。Stanford cs231n Lecture 10: Recurrent Neural Networks 的部分笔记。

引入

传统的神经网络中间层每一个神经元和输入的每一个数据进行运算得到一个激励然后产生一个中间层的输出，并没有记忆能力，在输入为序列的情况下的效果有限。而很多东西是受到时域信息影响的，某一时刻产生的激励对下一时刻是有用的，递归神经网络就具备这样的记忆能力，它可以把这一刻的特征与上一刻保存的激励信息相结合(并不只是上一刻 s2 是由 s1、s2 产生的，$s_n$ 不仅有 $s_{n-1}$ 的信息，还包括 $s_{n-2}$、$s_{n-3}$…$s_1$ 的信息。

CNN vs RNN:

  1. CNN 需要固定长度的输入、输出，RNN 的输入可以是不定长的
  2. CNN 只有 one-to-one 一种结构，而 RNN 有多种结构，如下图具体在下一部分再做介绍。
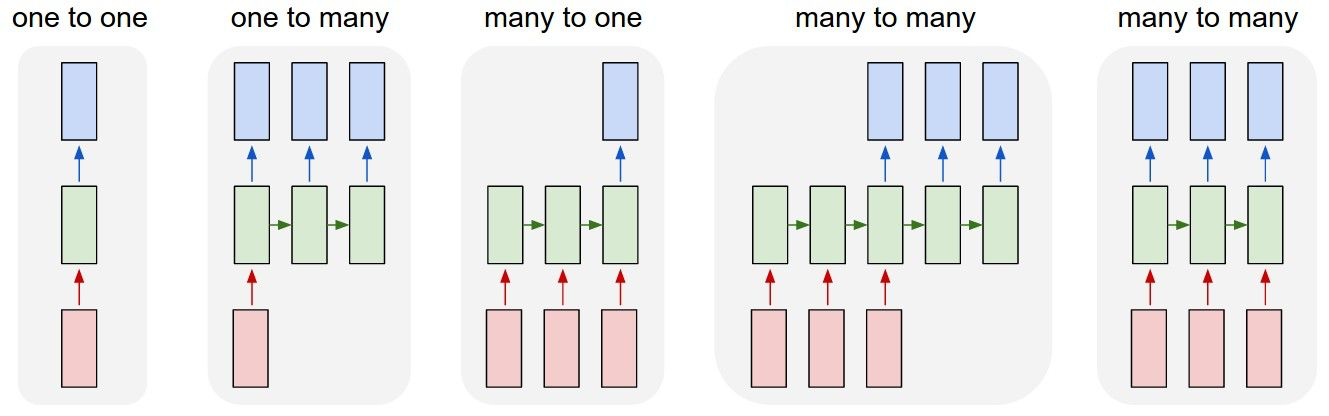
one_to_many.png

One-to-one: Vanilla Neural Networks
最简单的结构，然而效果不怎么好
One-to-many: Image Captioning, image -> sequence of works
​输入一个图片，输出一句描述图片的话
Many-to-one: Sentiment Classification, sequence of words -> sentiment
​输入一句话，判断是正面还是负面情绪
Many-to-many: Machine Translation, seq of words -> seq of words
​有个延时的，譬如机器翻译。
Many-to-many: Video classification on frame level
​输入一个视频，判断每帧分类。

Applications:

  • language models
  • translation
  • caption generation
  • program execution

RNN

基础

以 (Vanilla) Recurrent Neural Network 为例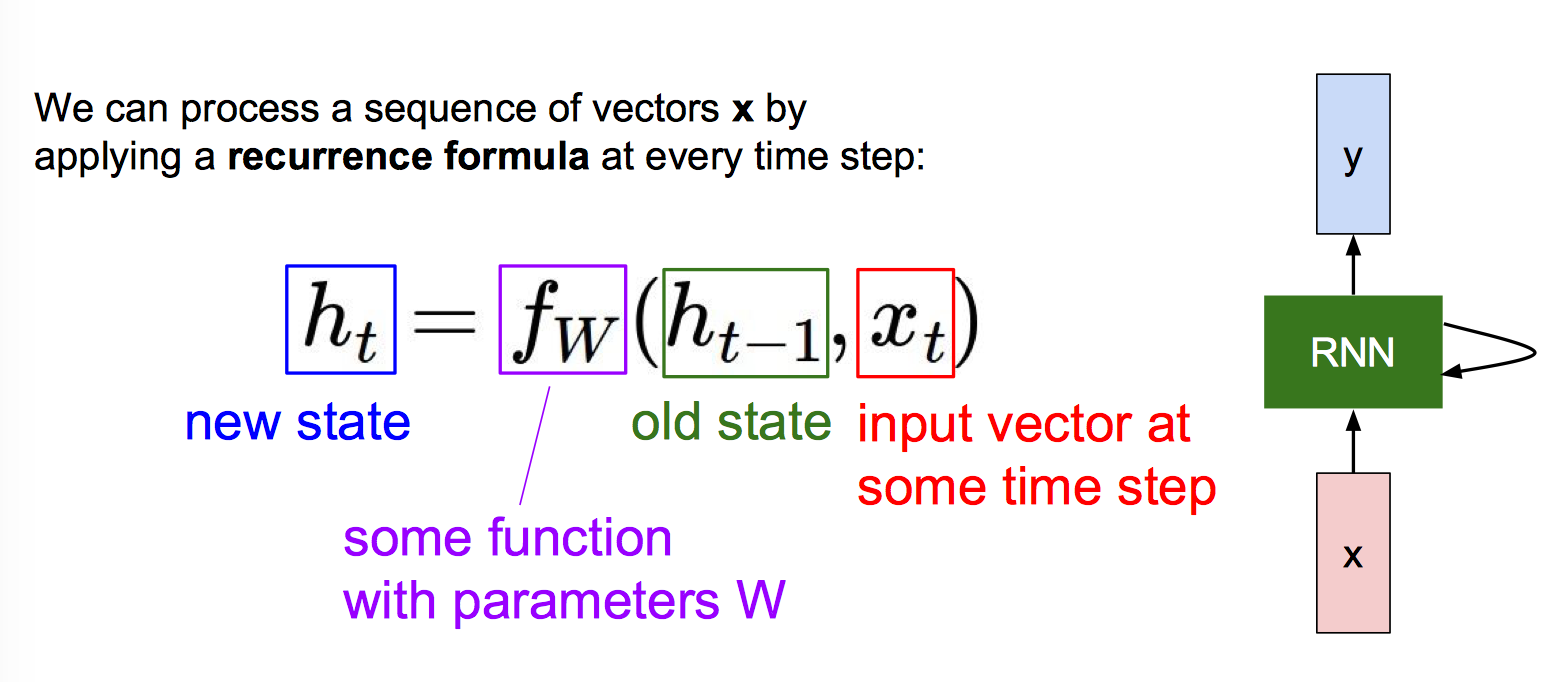
one_to_one.png

Forward(前向传播)

$$h_t=f_W(h_{t-1},x_t)$$

Notice: the same function and the same set of parameters are used at every time step.

$$h_t=tanh(W_{hh}h_{t-1}+W_{xh}x_t+b)$$
$$y_t=Softmax(W_{hy}h_t+c)$$

就是多加上 $h_{t-1}$，activation function 用的是 tanh

Backwards: Backpropagation Through Time(BPTT)
bptt.png
(请原谅我的字～) U 最大特征值(Largest singular value)大于 1 的时候，梯度爆炸，小于 1 的时候，则可能发生梯度消失。> 1 的时候还比较容易察觉，< 1 的时候往往难以发现了。
梯度爆炸可以采用Gradient clipping的方式(设个天花板)避免，如梯度大于 5 的时候就强制梯度等于5。梯度消散可以通过改变 RNN 结构如采用LSTM的方式抑制。

Loss function(损失函数)
Cross-entropy
$$E_t(y_t,\hat y_t)=-y_tlog \hat y_t$$
$$E(y_t,\hat y_t)=-\sum_t y_tlog \hat y_t$$

其他结构

经典 RNN 结构，输入和输出序列等长，适用范围比较小，比如 Char RNN，视频每一帧的分类任务等。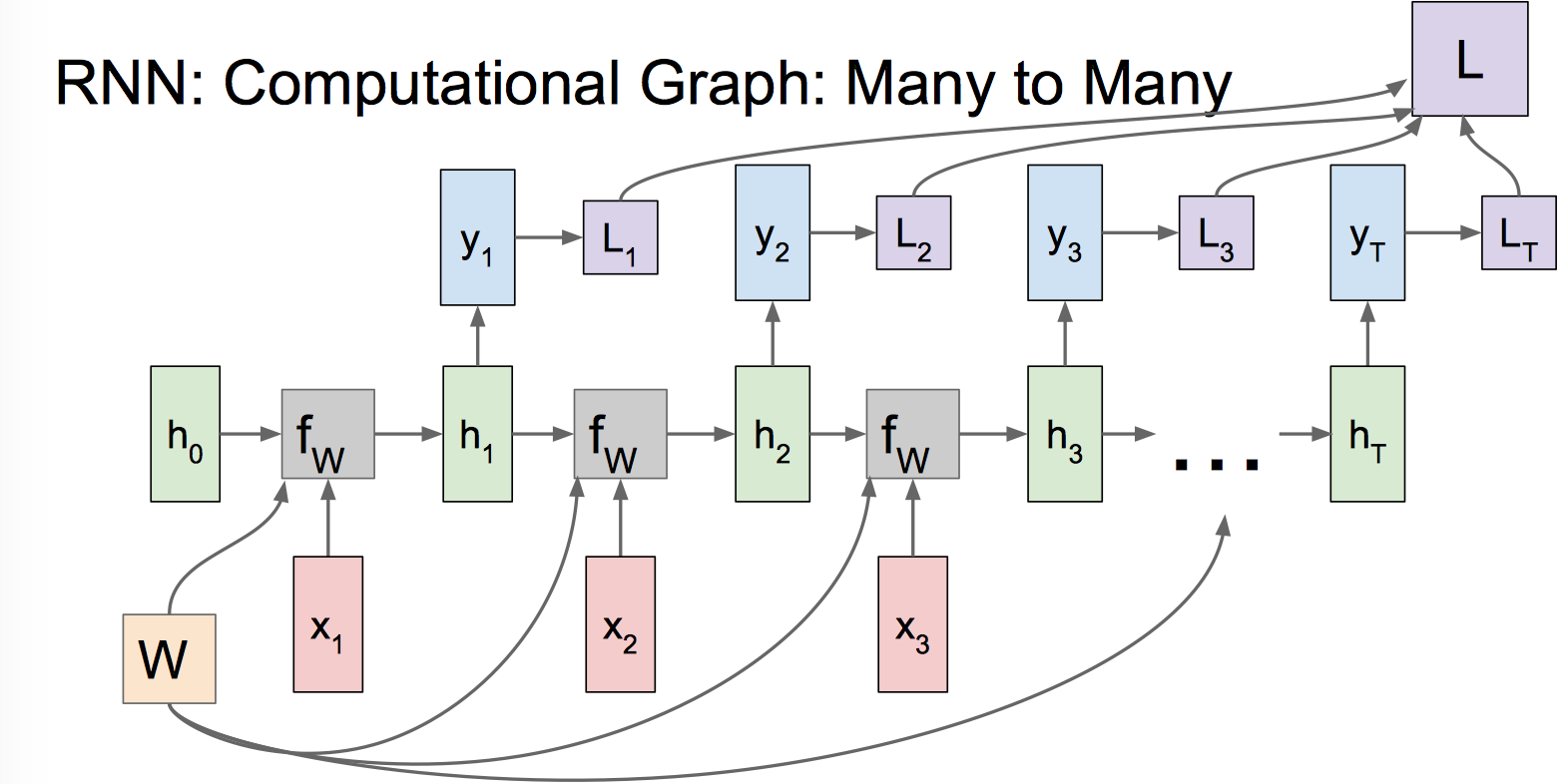
many_to_many.png

双向 RNN：输入信息一个正向，一个反向，原因是信息等依赖关系顺序不定。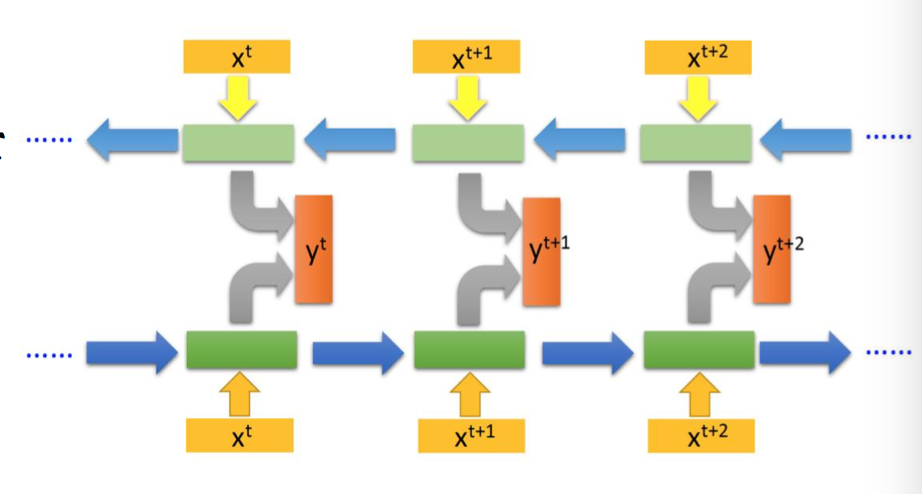
birnn.png

输入是序列，输出是单个值，通常处理序列分类问题，比如句子分类任务。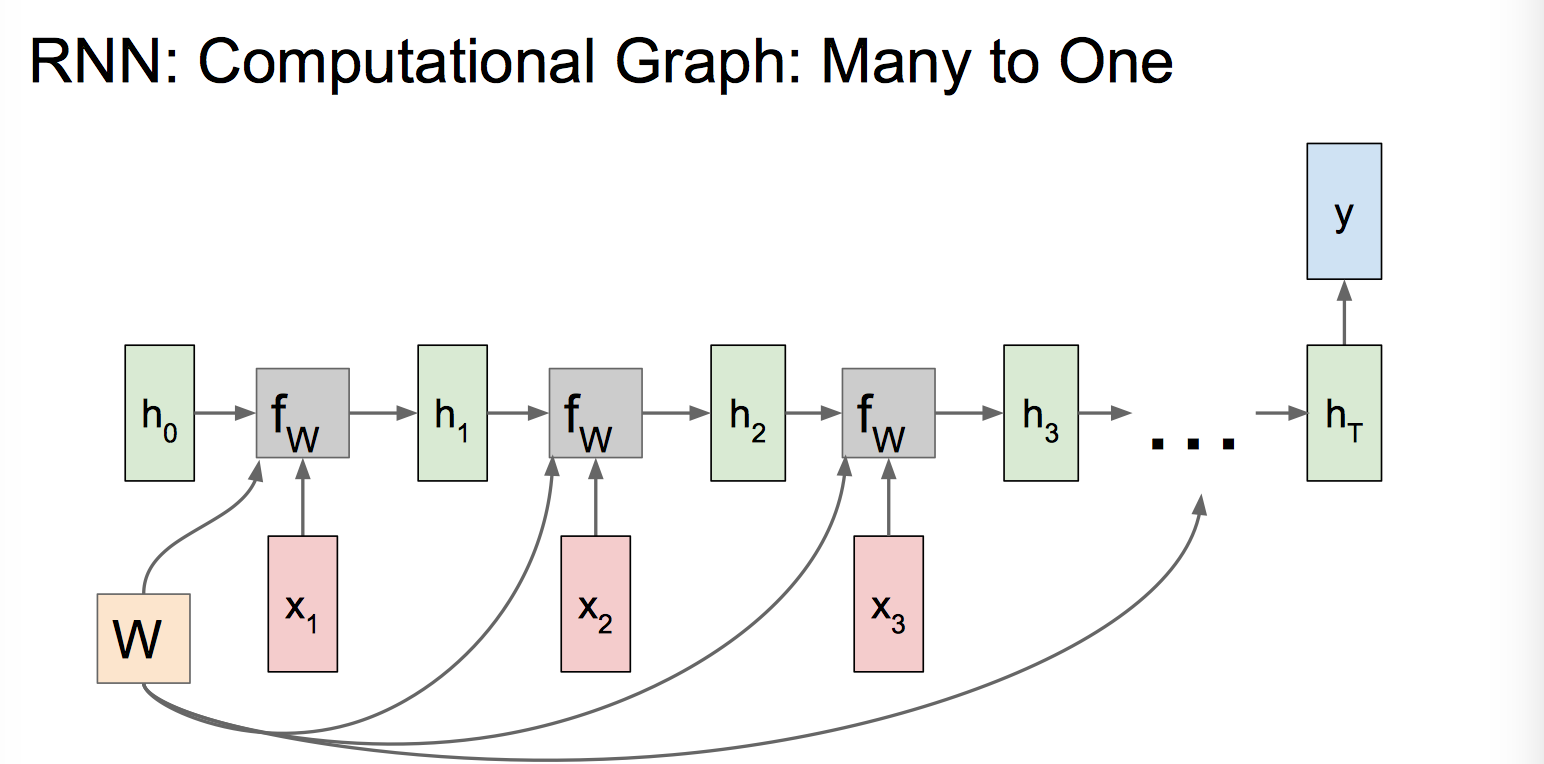
many_to_one.png

输入是值，输出是序列，decoder 时，可以把原始输入信息 X 作为序列输出开始的输入 ，也可以把 X 作为每个阶段的输入，可以处理 从图像/类别生成文字/语音/音乐 的问题，输入可以是 CNN 的 FC 层特征。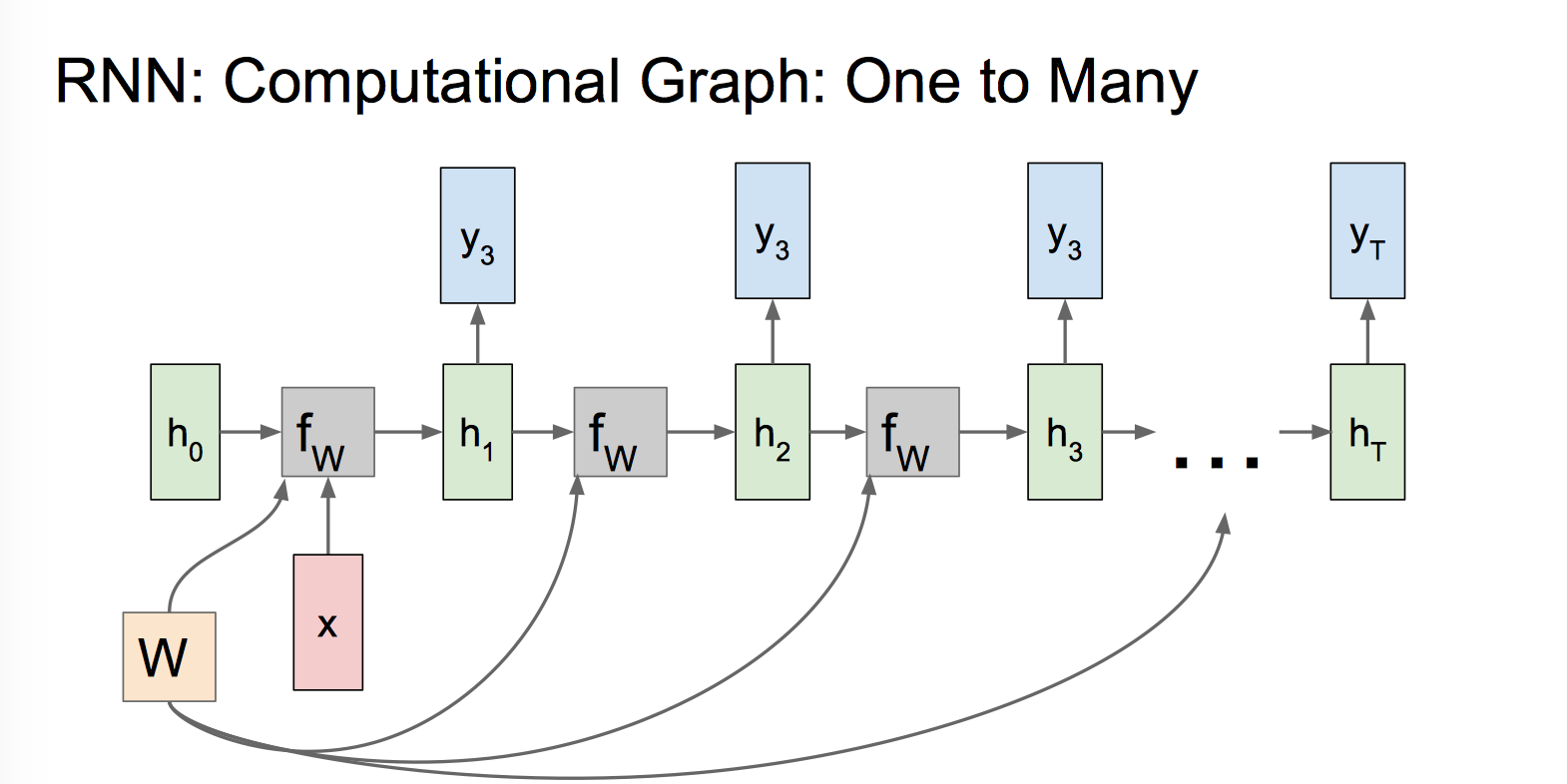
one_to_many_.png

经典的 Encoder-Decoder 或者说 Seq2Seq 模型，先用一个 Many-to-one 将输入编码成一个上下文向量 c，这个 c 可以是 Encoder 最后一个隐状态，也可以是这个隐状态的变换，还可以是所有隐状态的一个变换。有了 c，另一个 One-to-many 会对其进行解码，把 c 作为初始状态 $h_0$ 输入到 Decoder 中。这一部分也有各种变换，比如说把 c 当做 decoder 时每一步的输入。
Seq2Seq 结构应用非常广泛，在机器翻译、文本摘要、问答系统中都很常见。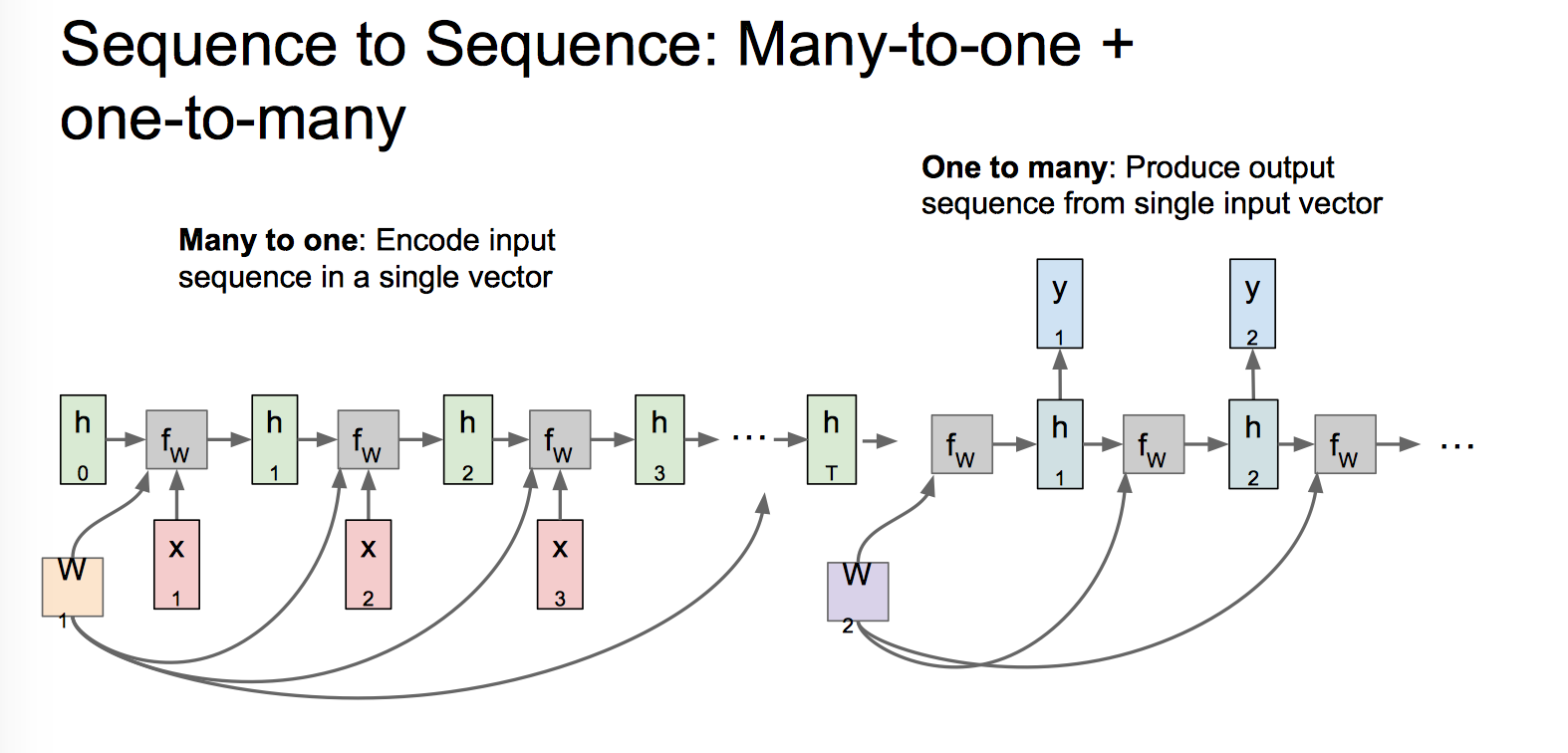
sequence_to_sequence.png

Example: Character-level Language Model Sampling

Vocabulary: [h, e, l, o]
Exaple training sequence: “hello”

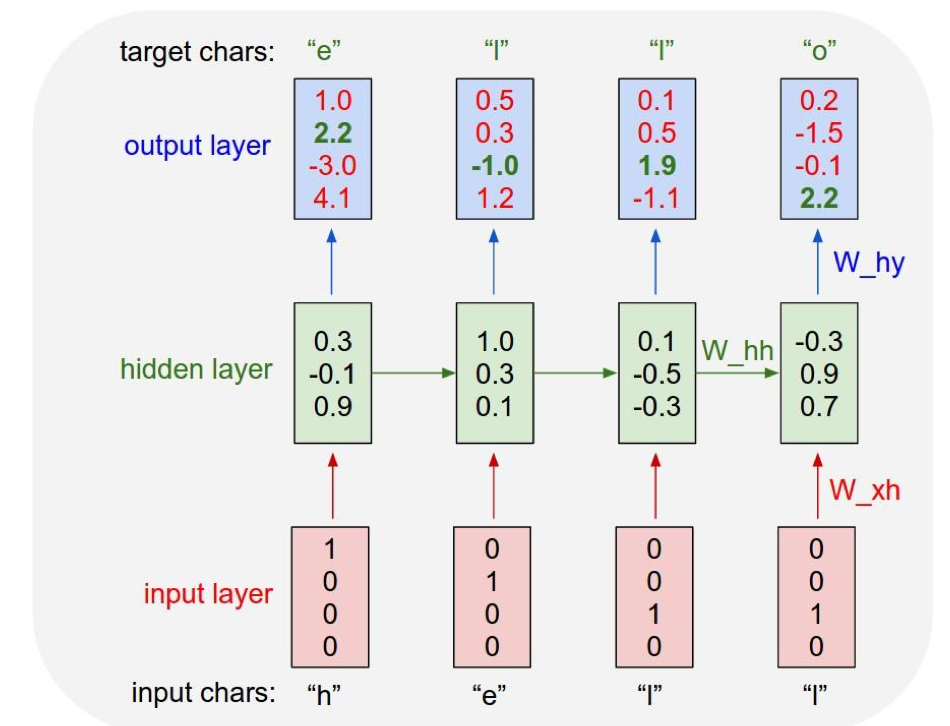
ch_lm_s.png

At test-time sample characters one at a time, feed back to model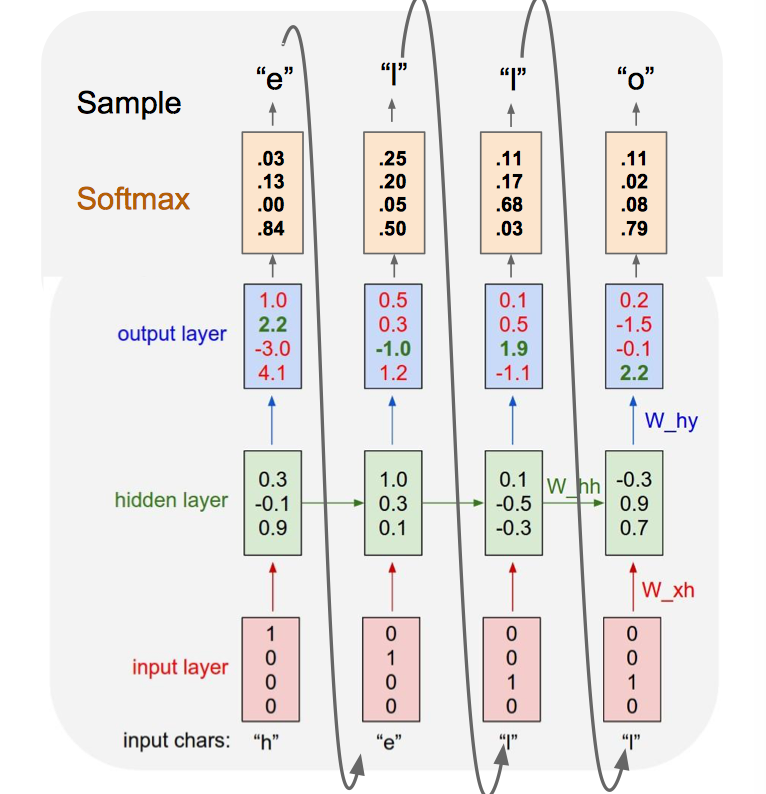
ch_lm_s2.png

Backpropagation through time:
Foward through entire sequence to compute loss, then backward through entire sequence to compute gradient.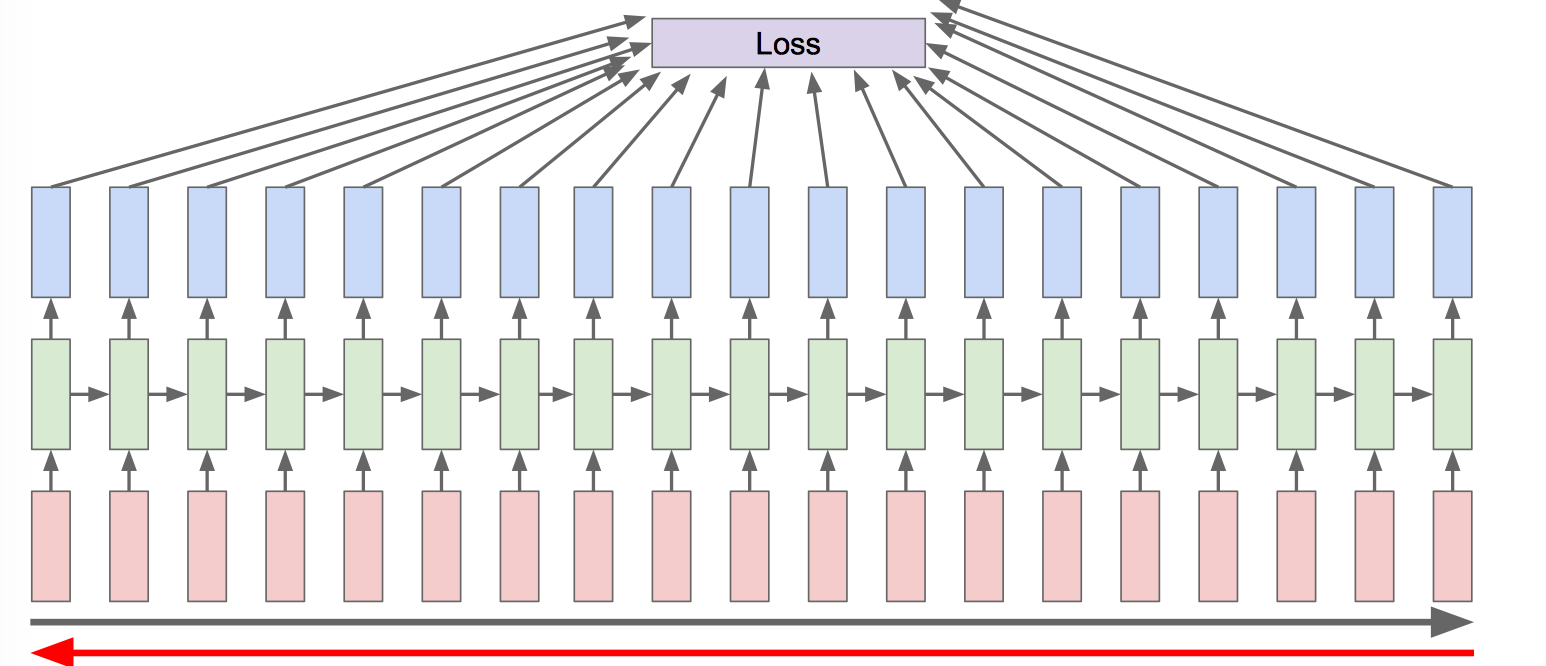
btt1.png

Truncated Backpropagation through time:
Run forward and backward through chunks of the sequence instead of whole sequence.
Carry hidden states forward in time forever, but only backpropagate for some smaller number of steps.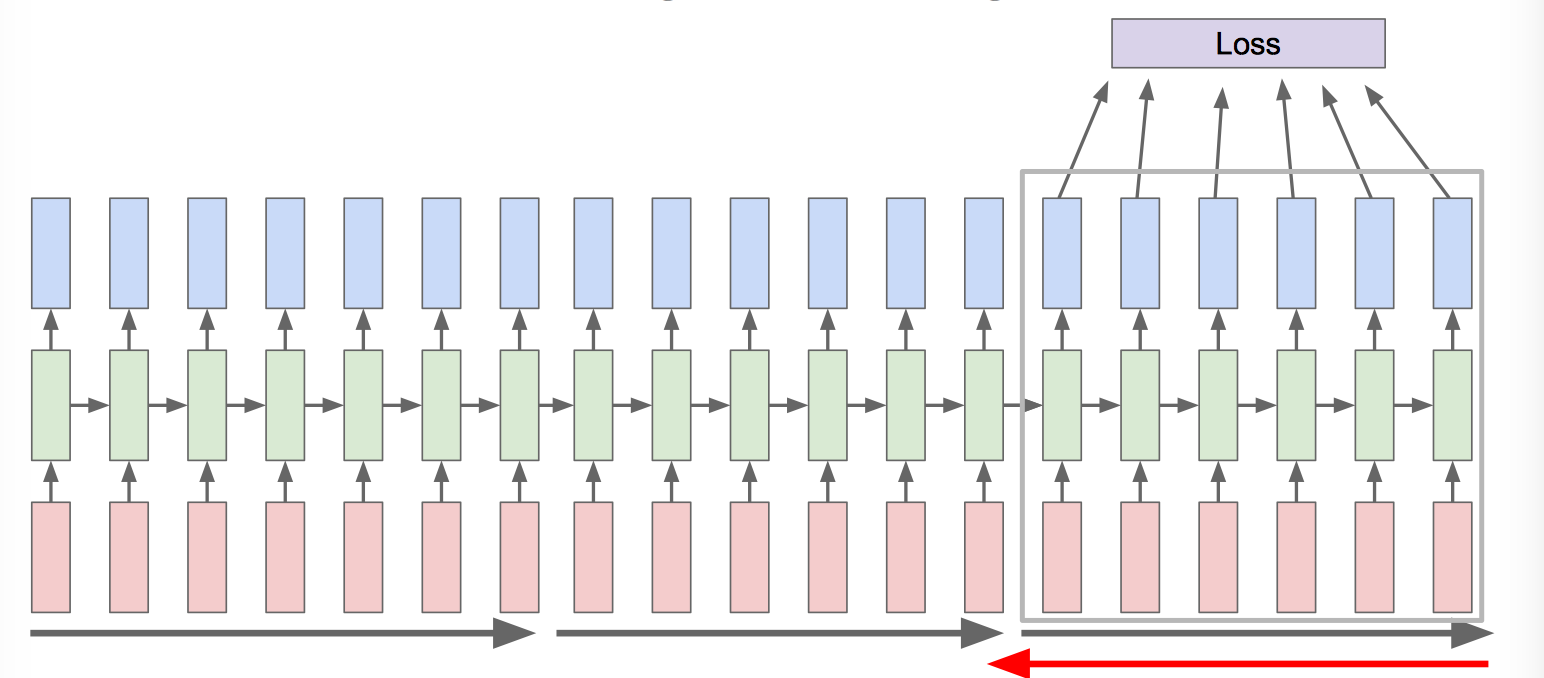
tbtt2.png

Image Captioning

可参考的 paper:
xplain Images with Multimodal Recurrent Neural Networks, Mao et al.
Deep Visual-Semantic Alignments for Generating Image Descriptions, Karpathy and Fei-Fei
Show and Tell: A Neural Image Caption Generator, Vinyals et al.
Long-term Recurrent Convolutional Networks for Visual Recognition and Description, Donahue et al.
Learning a Recurrent Visual Representation for Image Caption Generation, Chen and Zitnick

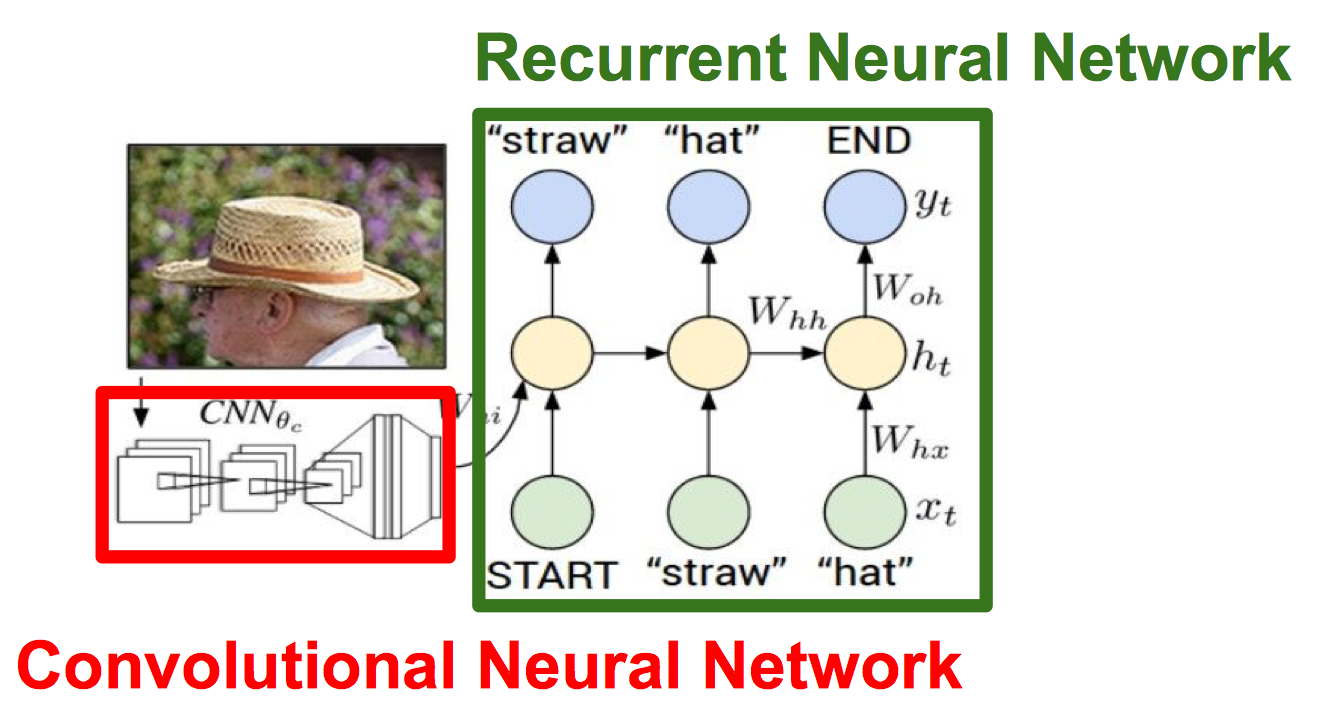
CNN%26RNN.png

下一篇重点解释。

RNN 局限

RNN 前后依赖的特性导致两个输入距离比较远的时候作用会非常弱，比如说下面的例子， China 对 Chinese 起决定作用，然而距离太远难以产生关联。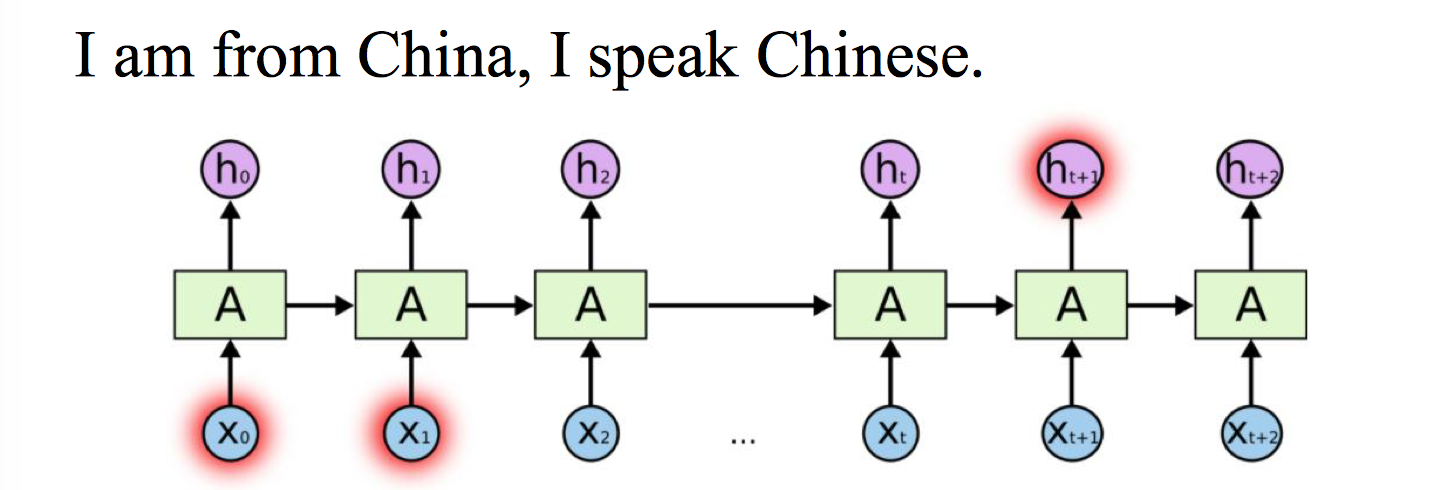
%E5%B1%80%E9%99%901.png

一个解决方案就是设计 Gate，保存重要记忆，也就是下面要讲的 LSTM，LSTM 网络模型解决了 RNN 梯度消散问题，同时保留了长时序列的相关性。

RNN 变种: LSTM

RNN 中重复的模块只有一个非常既简单的结构 tanh 层，而 LSTM 将重复模块改成了一个相对复杂的结构，这样可以有效避免梯度消失的问题。LSTM 要理解的核心是 GATE，它就是靠这些 gate 的结构让信息有选择性的影响 RNN 中每个时刻的状态。所谓 gate 的结构就是一个使用 sigmoid 神经网络和一个 elementwise multiplication 的操作，这两个操作合在一起就是一个门的结构，sigmoid 作为激活函数的全连接神经网络层会输出一个 0-1 之间的数值，描述当前输入有多少信息量可以通过这个结构，类似于门，门打开时(sigmoid 输出为1时)，全部信息都可以通过；当门关上时(sigmoid 输出为0)，任何信息都无法通过。

Vanilla RNN
$$
\begin{aligned}
h_t & = tanh(W_{hh}h_{t-1}+W_{xh}x_t) \\
& = tanh((W_{hh} W_{hx})\binom{h_{t-1}}{x_t}) \\
& = tanh(W \binom{h_{t-1}}{x_t}) \\
\end{aligned}
$$

看一下 Vanilla RNN 到 LSTM 前向传播的变化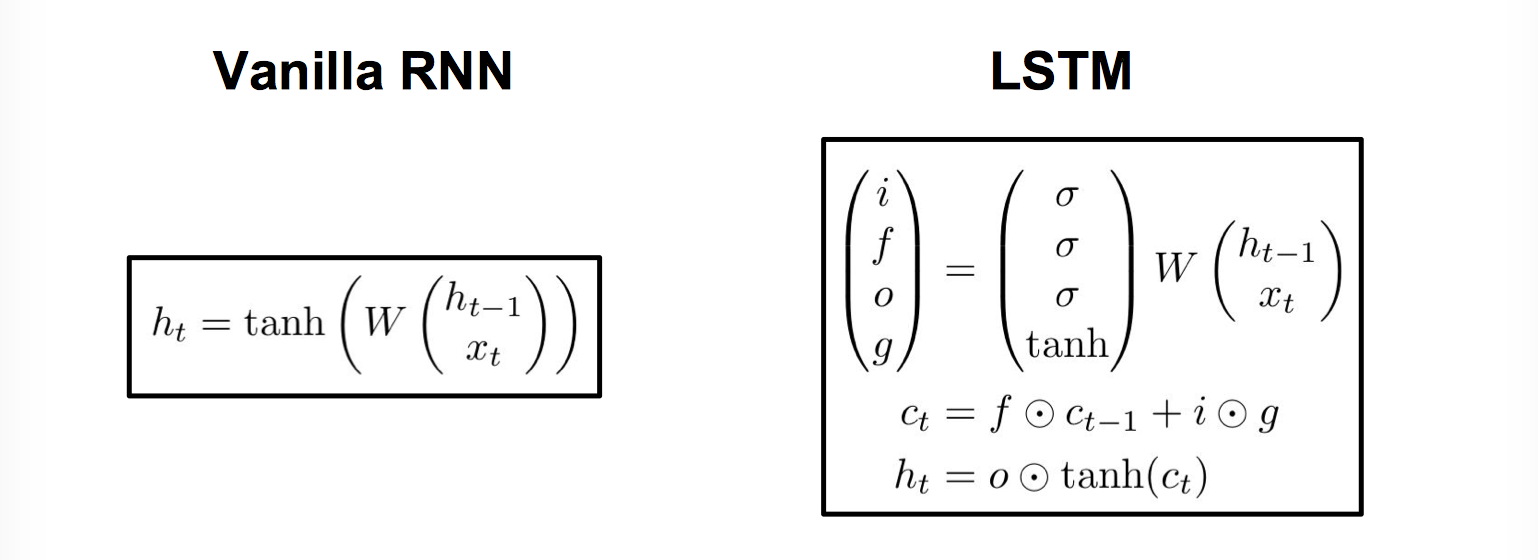
1.png

LSTM 网络结构图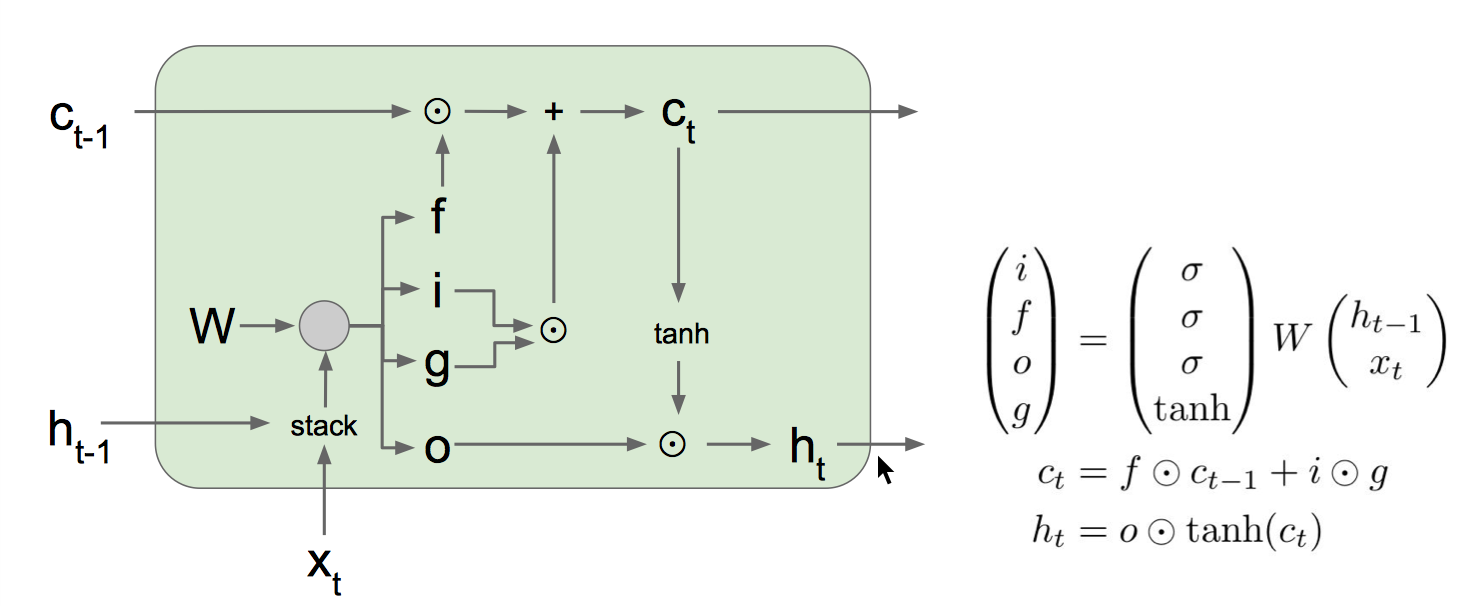
LSTMgate2.png

分步：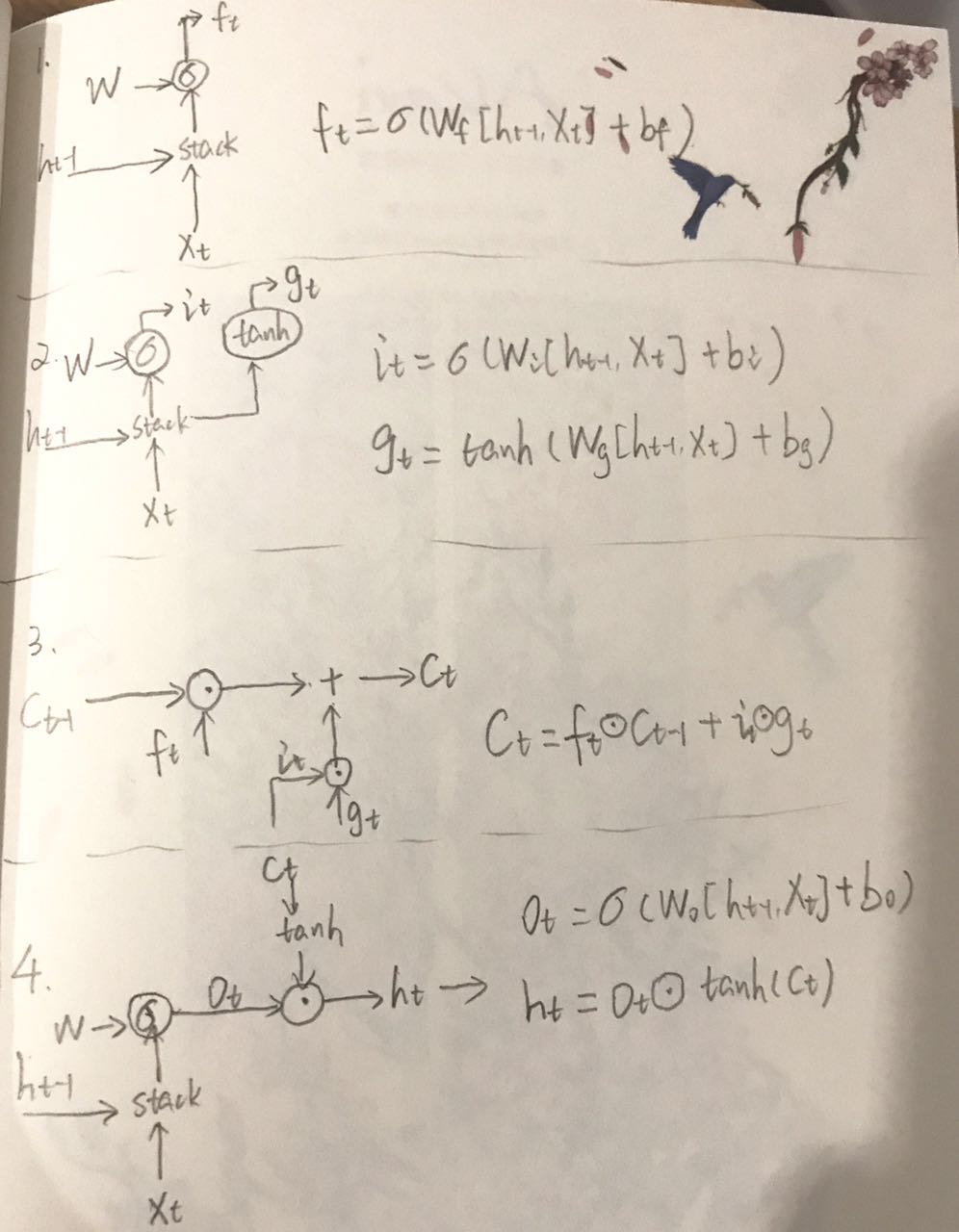
LSTMgate.png
f: Forget gate, Whether to erase cell
i: Input gate, whether to write to cell
g: Gate gate (?), How much to write to cell
o: Output gate, How much to reveal cell

Step 1:
decide what information we’re going to throw away from the cell state
新输入 $x_t$ 和前状态 $h_{t-1}$ 通过 sigmoid 变换决定 $c_{t-1}$ 的哪些信息可以舍弃，$f_t$ 与 $C_{t-1}$ 做 elementwise multiplication 运算，对部分信息进行去除

Step 2:
decide what new information we’re going to store in the cell state
新输入 $x_t$ 前状态 $h_{t-1}$ 通过 sigmoid 变换告诉 $c_t$ 哪些新信息想要保存，通过 tanh 变换建一个新的侯选值向量。
$i_t:$ 新信息添加时的系数(对比 $f_t$)，$g_t$ 单独新数据形成的控制参数，用于对 $C_t$ 进行更新。

Step 3:
update the old cell state
根据旧的控制参数 $C_{t-1}, f_t, i_t, g_t$ 组合生成最终生成该时刻最终控制参数

Step 4:
decide what we’re going to output
新输入 $x_t$ 和前状态 $h_{t-1}$ 通过 sigmoid 变换决定 cell state 的哪些信息需要输出，与 cell state 通过 tanh 变换后的值相乘，产生此刻的新的 LSTM 输出

核心内容 $C_t$，信息流控制的关键，参数决定了 $h_t$ 传递过程中，哪些被保存或舍弃，参数被 Gate 影响。怎样实现 Gate 对 C 影响？ Sigmoid 函数系数据定 $C_t$ 参数的变化，而 Sigmoid 函数决定于输入。
整个过程：$C_t$ 信息舍弃 => $C_t$ 局部生成 => $C_t$ 更新 => $C_t$ 运算

Backpropagation: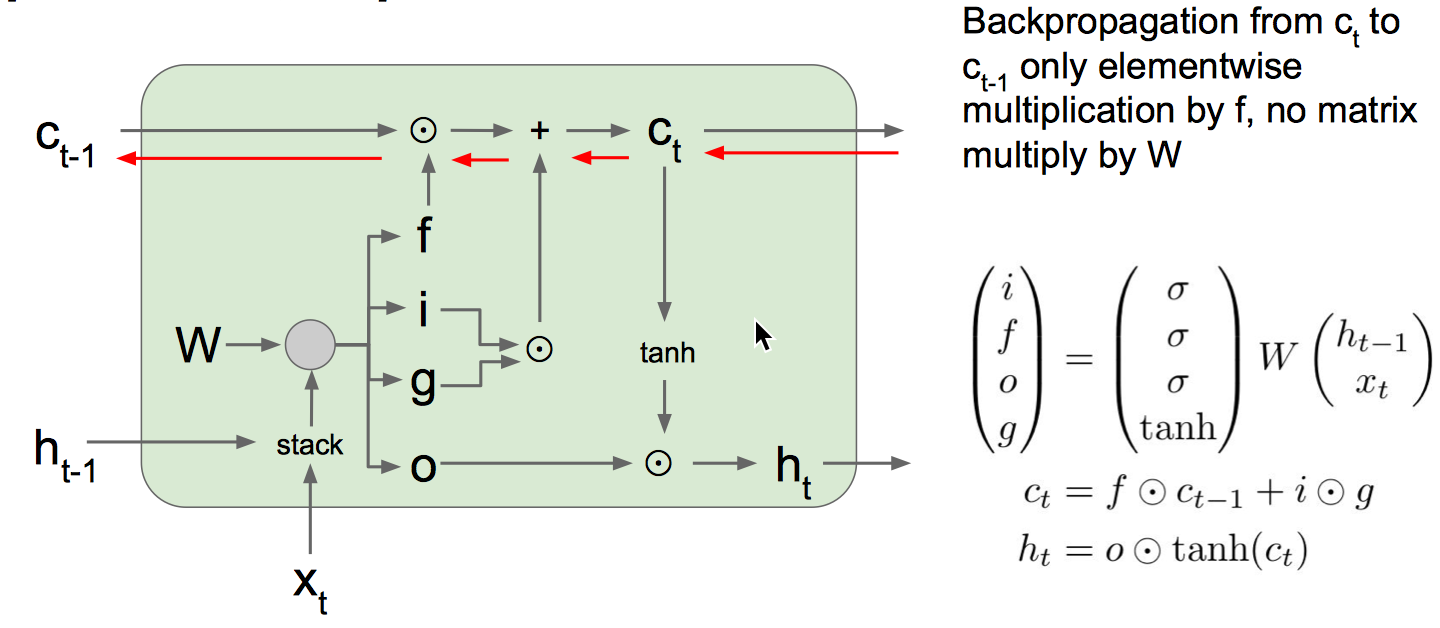
LSTMbp.png

LSTM 变种: Peephole connection

$C_t$ 受到 Gate 参数影响 => 二者相互影响
$f_t=\sigma(W_f[C_{t-1},h_{t-1},x_t]+b_f)$
$f_t=\sigma(W_i[C_{t-1},h_{t-1},x_t]+b_i)$
$f_t=\sigma(W_o[C_{t-1},h_{t-1},x_t]+b_o)$

LSTM 变种: 遗忘/更新互为补充

Gate 的 遗忘/更新 不再独立，而是互为补充。

$C_t = f_t * C_{t-1} + i_t * g_t$ => $C_t = f_t * C_{t-1} + (1-f_t) * g_t$

LSTM 变种: GRU(Gated Recurrent Unit)

  1. 遗忘，更新 Gate 结合(不是独立，也不是互补)形成更新门
  2. 控制参数 $C_t$ 与输出 $h_t$ 结合，直接产生带有长短记忆能力的输出 linkGRU.png

小结

  • RNN 应用在 language model 中，学习的实质是 P(下个词|前面多个词)
  • Vanilla RNNs 非常简单，但效果不好，通常会使用 LSTM 和 GRU，这两种结构能提高 gradient flow
  • 在一层 RNN 中不同时间序列中激励函数和权值参数都一致
  • RNN 也可以是多层 RNN，其网络是整个一模型一起训练的
  • RNN 存在着梯度爆炸和梯度消散的问题。梯度爆炸可以采用Gradient clipping的方式避免，梯度消散可以采用 LSTM 的网络结构抑制
  • 中间层的特征带有前后时间特征，对一些任务很有用
  • 额外参数：单双向/梯度上限/梯度计算范围
徐阿衡 wechat
欢迎关注：徐阿衡的微信公众号
客官，打个赏呗~